We encounter cartels on a daily basis in our free time, through blockbuster TV series such as AMC’s Breaking Bad and Netflix’ El Chapo. However, cartels also affect us in our daily lives in other ways, although they tend to revolve around different commodities.
Most organised forms of collusion, like drugs cartels, are illegal and lead to dire consequences, particularly when they span over a number of international legal territories, as financial penalties accrue exponentially.
WHY DO CASES OF NON-TACIT COLLUSION OCCUR SO FREQUENTLY?
Microeconomic theory explains this with an easy calculation. Take the excess profits gained by a monopoly over the competition and distribute it across all participants. If this figure is higher than the expected penalty payment, it makes sense for a company to risk collusion.
INDEMNITY MUST BE CLAIMED BY THE VICTIMS
Whether collusion (whereby companies repeatedly interact with one another) can be stable, has been widely assessed through game-theoretical approaches. Many cases of instable cartels make it to the news, when at least one participant retracts from their collusive agreement and reveals the affiliation to the authorities. In many jurisdictions, this “chief witness” is exempt from a penalty given by the competition authorities. In any case, indemnity is available to all parties who suffered damage, but it must be actively claimed by the victims. More often than not this leads to arduous and expensive bilateral negotiations, where each participant tries to “out do” each other by issuing red tape in the form of legal and economic assessments. The worst-case outcome of these negotiations is failing to repatriate forgone earnings, leaving a bad atmosphere between the participants, which potentially taints any future co-operation. That said, companies who face wrongdoing from their partners should not refrain from claiming their rights. However, this needs to be handled in a structured and transparent way in order to avoid these pitfalls. Game theory proposes a procedure to achieve just that. Adopting a game-theoretical approach offers the possibility to systematically analyse repeated interactions between economics subjects, such as companies, and derive an approach depending on the strategic alternatives of all relevant participants. The resulting strategy is global and follows a structured, “if-then” roadmap, which is uniform and simultaneous across all counterparts.
APPLYING GAME THEORY TO A RECENT CASE
Applying game theory to the recent case of outstanding claims by Deutsche Bahn, due to an illegal cartel in the area of air cargo, provides a perfect example. As described in an article by the F.A.Z., Deutsche Bahn recently agreed on a settlement with Lufthansa of less than 50m EUR, to redeem its participation in the cartel after more than six years of negotiations. After colluding on fuel and security surcharges between 1999 and 2006, the cartel was disclosed by Lufthansa who then managed to escape from paying any penalty payments to the European Commission due to their status as chief witness. With the legal foundation laid out by European and US court rulings, Deutsche Bahn set out its quest for indemnity from eleven collusive air cargo carriers which amounted to 1.76bn EUR. With Lufthansa’s payment amounting to just 50m EUR, this appears rather small in the light of their importance in the process, as well as the length of the negotiation. Indemnity claims towards six other carriers still remain open and, understandably, the responsible board member Martin Seiler emphasised that “it would be better for everyone if [Deutsche Bahn] could also reach an agreement with the other cartel participants instead of having costly court proceedings for years”.
A PREDICTABLE PROCESS OF ACTION AND REACTION ALTERNATIVES
Conventional strategies with respect to indemnity claims focus on deciding whether to go for the big fish first, or to start out with smaller counterparts who have a higher willingness to pay. In contrast, a game-theoretical approach considers the entire set of actions of each individual “player” and relates them to each other. So, instead of agonising over the opportunity cost of quick money, the game-theoretical approach would achieve just what Mr. Seiler desires. A predictable process of action and reaction alternatives, depending on every participant’s alternatives, which is transparent enough to ensure future relations and has the highest likelihood to reach an efficient outcome for all “players”. To achieve this, it is critical that four distinct steps are followed:
- Game tree
- Outcome determination
- Backward induction
- Correct implementation
1. GAME TREE
Firstly, a game tree needs to be set up. This is an extensive form which describes the key action and reaction alternative of all relevant players. Here, it is crucial to move from one step (or “node”) to another by diligently assessing the respective player’s opportunities, so that they are collectively exhaustive as well as mutually exclusive.
Figure 1 below shows a simplified game tree, where Deutsche Bahn (DB) has the chance to file a lawsuit or make an offer to its counterpart Lufthansa (LH), which would result in a private settlement if accepted. Depending on DB’s choice, LH has the chance to accept or reject DB’s offer. Or, if DB chooses the lawsuit, LH cannot respond in this step as they would move to court directly. In round 3, DB would, depending on the previous actions, make an offer or file a lawsuit against another participant from the cartel (i.e. the 3rd party) and so on. This example, for illustrative purposes only, considers just two counterparts and only four steps of interaction. A sufficiently sophisticated game tree would include simultaneous actions towards multiple counterparts, as well as infinite interaction between the players, in order to take business relations after the court settlement into account.
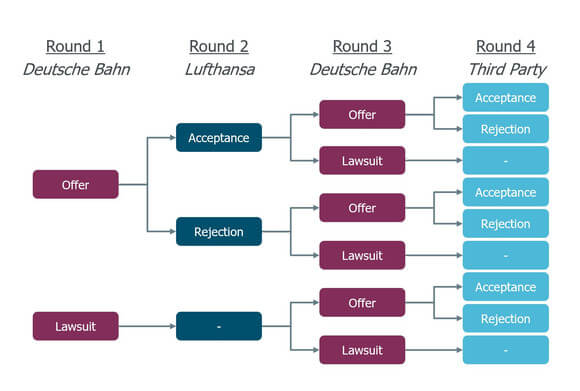
While infinite interaction might appear cumbersome in a finite negotiation such as this, game theory addresses this by introducing discount factors, making events in the far future less relevant for today’s decisions.
2. OUTCOME DETERMINATION
Secondly, the outcome (or “payoffs”) of each possible combination of actions needs to be determined. This process requires thorough assessment of the respective case, as well as educated predictions of expectable gains from court decisions, costs of legal and economic support, and potential harm to business relations that litigation would imply. Any uncertainties within the process need to be adequately translated into probabilities.
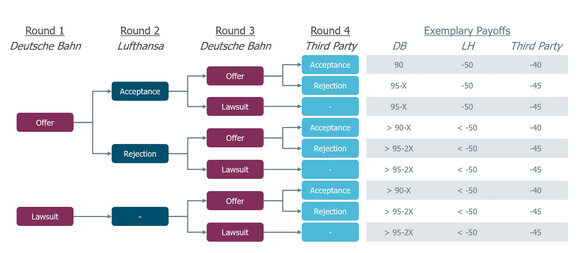
Figure 2 below, shows exemplary payoffs in millions of Euros are assigned to each possible set of outcomes, while “X” refers to Deutsche Bahn’s cost in a legal dispute. For the purpose of this example, it is assumed that Deutsche Bahn gains 50m EUR from Lufthansa and 40m EUR from another (smaller) counterpart if an offer is accepted. Conversely, it is assumed that a lawsuit would yield less than 50m EUR from Lufthansa and 45m EUR from the other third party. If it comes to a lawsuit, however, Deutsche Bahn always has to invest Xm EUR, reducing its overall gains.
3. BACKWARD INDUCTION
Thirdly, the optimal combination of strategies for Deutsche Bahn has to be identified, taking the set of action alternatives of all other players into account. The resulting so called “subgame-perfect equilibrium”, as introduced by Reinhard Selten, a German laureate of the 1994 Nobel Memorial Prize in Economic Sciences, can be determined through a straightforward game-theoretical method called “backward induction”. This means looking at the final decision, as well as their corresponding payoffs, and moving backwards from the respective profit maximising outcomes. In this example, the third party in round 4 has the final decision to make, which depends on whether they have to pay 40 or 45m EUR. If the preceding rounds resulted in an offer for the third party, they will always choose to accept as it will save them 5m EUR. Similarly, Deutsche Bahn will determine their optimal strategy in round 3 depending on the alternatives that are still open and the certainty that the third party will always accept an offer, and so on. Ultimately, Deutsche Bahn in round 1 will be able to identify the strategy which will maximise its profit, considering which actions will be “played” in later rounds. In this case, the optimal strategy depends on the expected cost of a lawsuit, ‘X’. If the cost of the lawsuit is below 5m EUR, Deutsche Bahn will choose to make Lufthansa an offer and file a lawsuit against the third party, in order to receive a payoff larger than 90m EUR. Lufthansa will accept in order to avoid costs of more than 50m EUR in a lawsuit, and the 3rd party cannot accept an offer and decrease Deutsche Bahn’s profit. Conversely, if the cost of a lawsuit exceeds 5m EUR, Lufthansa will make offers to both counterparts which they will accept, and earn 90m EUR.
4. CORRECT IMPLEMENTATION
Fourthly, the correct implementation of the identified strategy needs to be ensured for which two elements are key. One, the determined strategy needs to be followed and it needs to be credible so that no deviations will occur. Two, all counterparts need to understand their scope of action as well as their consequences; i.e. information asymmetry has to be eliminated. While the latter can be achieved through transparency and clear elucidation when it comes to their situation, Deutsche Bahn must make a commitment which will leave no doors open to manoeuvre into a different direction. In practice this can pose a challenge, as some participants in negotiations have a preference to leave doors open so as not to “burn bridges”, just in case something goes amiss. This can be seen in classical situations that have been analysed via game theory, such as the “chicken game”. In this game, two people are driving towards each other to see who moves or “chickens out” first. In an extreme method to demonstrate their willingness to go to the very end, one driver could destroy their steering wheel. Even though this might seem crazy, this radical form of “signalling” achieves exactly the needed degree of commitment. Naturally, in real life, the worst possible outcome needs to be altered to an acceptable level upfront.
REDUCE DAMAGE
So for Deutsche Bahn, as much as any other party fighting for their redemption, following this game-theoretical approach could facilitate their aspirations as well as significantly reduce damage to any future business relations.
