Discussions about the efficiency of Christmas gifts is quite an interesting topic for economists.
Some may claim that giving money would be the most efficient gift, as the recipient knows best what to spend it on (rather than for example receiving a gift worth $50, which they value at only $25), but views on this are divided.1
In this blog article we won’t look at what is the best present to buy, but instead focus on who should provide whom a present. Specifically, we will look at a tradition carried out every year in many companies called “Secret Santa”. For those of you unfamiliar with it, the basic idea is:
- A number of people take part, e.g. everyone in department X.
- Each person gets assigned one other person in the department.
- You send your assigned person a Christmas gift.
- Everyone receives a gift from a Secret Santa.
- Depending on how this is set up, it may or may not be revealed at the end who was the sender of any particular gift.
Now the participants may have preferences on both whom to give a present to and from whom they would like to receive a present, for example:
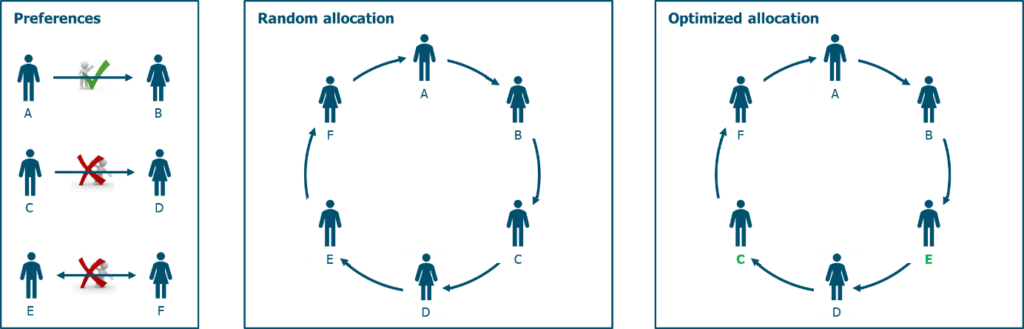
- Person A, a Manchester United supporter, has – in their eyes – the perfect present for person B, a Bayern Munich supporter (namely a DVD of the 1999 Champions League final).
- Person C got assigned Person D two years in a row and, due to having run out of ideas, would this time like to pick a present for somebody else.
- Persons E and F are a couple and they’d rather get assigned somebody else in the team to make it interesting.
Now what is the best way for incorporating such preferences in the allocation procedure? Let’s see whether we can get some insights from applying learnings from Matching Theory, a field of economics!
Option 1) Random allocation

The most commonly practiced option is a simple random allocation. Back in the days when people still met up for work face-to-face, a typical way to resolve this would be everyone drawing names out of a hat. It has to be said that there are some operational difficulties with this (as you are not meant to pick yourself!), but let’s not dive into this.
This approach has some merits, as it is fair (everyone gets the same chance to get assigned everybody else) and relatively simple to conduct.
On the downside however, this approach does not consider any of the preferences as mentioned above. Let’s use the examples from above and assume A -> B -> C -> D -> E -> F -> A was the resulting allocation. Persons E and C could both improve on the resulting allocation by swapping their assigned person.
Let’s look into some alternative approaches and see if we find one where no such trades are possible, resulting in an allocation that Matching Theorists call ‘stable’.2
Option 2) Building pairs

With an even number of participants, one could use a procedure based on an algorithm originally proposed for the ‘roommate problem’:
- Everybody submits a ranking (1 to n-1) about all other n-1 participants potentially to be paired with.
- The Irving algorithm3 (an explanation how it works would break the limits of this post here – those interested will easily find more information in the web) is used to find a stable matching of n/2 pairs – if it exists.
- The pairs exchange gifts.
Now a mechanism that arrives at a stable matching is something highly desirable in Matching Theory and has proven so in practice. Furthermore, this approach considers both preferences for sending as well as receiving.
But there are downsides, meaning this approach is problematic in practice:
- We can only use the mechanism for even numbers (as we do not want anybody to be left unpaired).
- This approach completely removes the ‘secret’ element, as once you know whom to send the gift to, you know that they are the person giving you a gift.
- The existence of a stable matching is not guaranteed. If no stable matching exists, then the Irving algorithm returns no allocation at all. That would be quite disappointing, as we would not want to call off the whole Secret Santa.
So is there an alternative that guarantees a desirable result?
Option 3) Random serial dictatorship

Firstly, we need to decide which preference side is most important – a) the person to receive the gift from or b) the person to send the gift to. Let us say we go for b) (the logic works analogously if we pick a), of course).
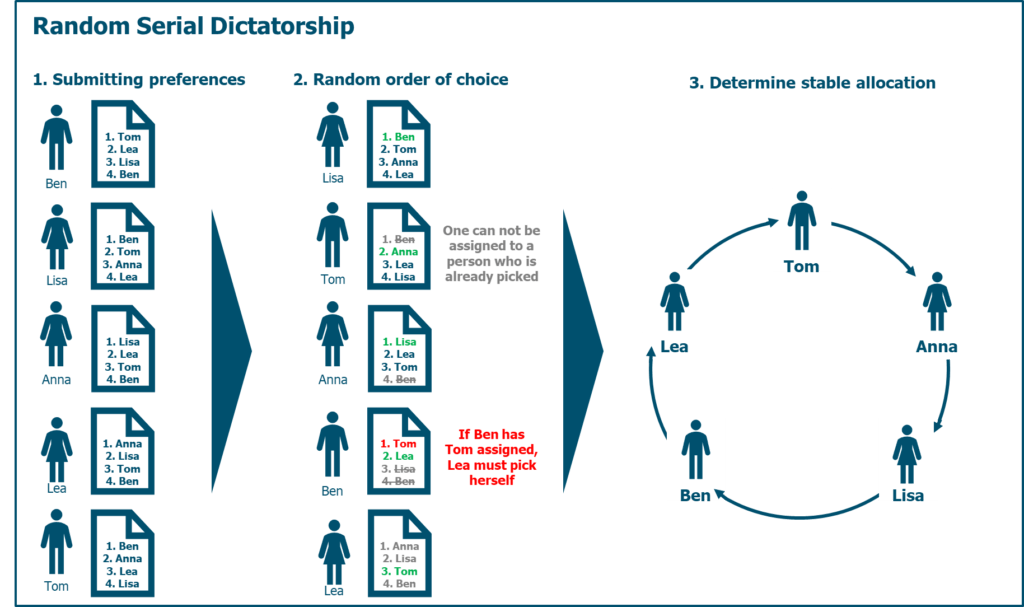
We can then run a procedure known as the Random serial dictatorship4 algorithm, which works as follows:
- Everybody submits a ranked list of whom they would like to send a gift to.
- Then we draw a random order of choice.
- The first person in this order gets assigned their number 1 rank from their preference list.
- Everybody else in this order gets assigned their highest rank that has not been picked already by somebody else with a higher order of choice. Now, we need to amend this known algorithm, to ensure that the last person to pick is not left to pick themselves. So we add the following rule:
- The second to last person in the drawn order of choice is assigned the last person in the order of choice, if that person is still unassigned.
This procedure has some merits:
- The result is feasible (everyone gets assigned one person to send a gift to).
- The algorithm is fair (everyone gets the same chance to pick first).
- It is strategy-proof (there is no reason not to submit your true ranking).
- It is stable with respect to the direction of preference used (everybody who picked higher up the hierarchy picked someone they prefer over your choice).
The main downside is that it only considers one direction of preference – sending or receiving.
Conclusion
The options above are of course not exhaustive (the interested reader may for example consider a fitting adaptation of the so-called TTC5 algorithm), but we hope to have provided some ideas on how you could try to use concepts from Matching Theory in Secret Santa.
However, if you do, a word of caution – you will also need to consider the means of implementation. Participants submitting preferences typically would not like to disclose them (e.g. to the organiser of such game) or like to know when they were picked (nobody likes to get picked last for a football team!).
So, if you do anything else but random selection, then having a system set up that conducts the allocation automatically and only informs each participant at the end about their match, would be really crucial to its success.
On this note … Merry Christmas & Happy Holidays!
Sources
1) Christmas gifts: See for example “Is cash the most ‘efficient’ Christmas gift?” – The Week
2) Stability: See “College Admissions and the Stability of Marriage” (D. Gale & L. Shapley, 1962) – The American Mathematical Monthly
3) Roommate problem: See “An efficient algorithm for the ‘stable roommates’ problem” (R. Irving, 1985) – Journal of Algorithms
4) RSD: Introduced in “Random Serial Dictatorship and the Core from Random Endowments in House Allocation Problems” (A. Abdulkadiroglu & T. Sonmez, 1998) – Econometrica
5) TTC (Top Trading Cycles): Introduced in “On Cores and Indivisibility” (L. Shapley & H. Scarf, 1974) – Journal of Mathematical Economics
