The data scientist guide to unnecessarily complicate little things in life.
Last week, a couple of friends and I split an Uber after dinner as our destinations were on the way. I requested the ride and paid for it since I was the last drop-off.
End of story, right?
Nope. My friends insisted on splitting the fare with me.
I initially thought of splitting the fares equally using the Uber Split Fare feature. The problem with an even split, however, is that it’s not fair to the person who gets drop-off first to split the ride — they would be better off getting a separate ride!
I soon found myself going on a thought spiral. How do I split the fares fairly? What is fairness anyway?… Do I believe in equal opportunity or equal outcome?
I eventually figured it out. I’m writing this post so when someone googles “How to optimally split an Uber ride”, they will find it here and know that they are not alone.
Before scrolling further, feel free to take a moment and think about how you would go around splitting the fare.
You will need the information in the image below. These are actual data (rounded up) — I got the fares for each trip by entering different pick-up and drop-off spots on Uber. (C is my drop-off)
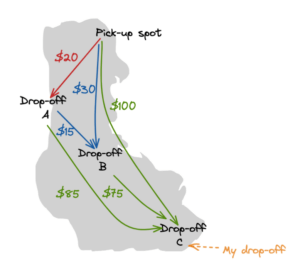
Hand drawn map of SF Bay Area
Introducing Shapley value
It turns out that my problem can be answered elegantly by a game theory solution concept called Shapley value.
For the ML partitioners, you may know about it from the SHAP python library for interpreting model outputs.
What is Shapley Value
The Shapley Value is a gaming theory that posits that gains and losses (costs) of a game should be distributed fairly amount all the actors who worked collaboratively. This theory is a solution theory used in a context where there is cooperation or coalition amongst all the actors in a particular task.
The Shapley value is the average of all the marginal contributions to all possible coalitions.
For our use case, applying Shapley Value means each rider will only pay what is necessary for them at the maximum.
Using Shapley value will satisfy the following two fairness clauses:
- Individual rationality: each rider pays less than the cost of taking their ride
- Pairwise rationality: each rider pays less than any alternative combination of rides. eg: fare for trip(A, B) <= fare for trip(A,B,C) for both A and B.
The solution
To calculate the Shapley value for our split fare problem, we will need to calculate the marginal fare for each possible order, and take the average fare for each rider at the end.
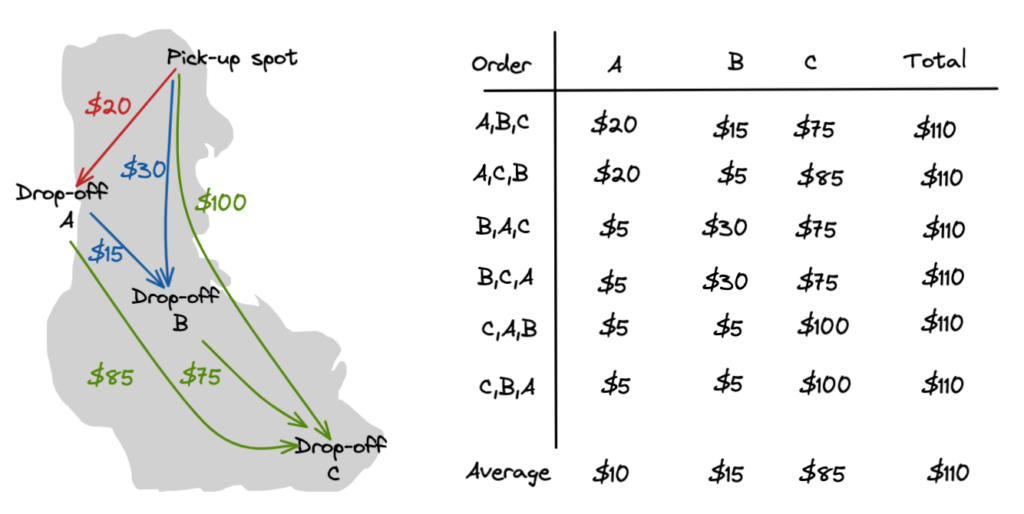
List of all permutations. The Shapley value is the average for each rider (last row)
For example:
- Order(A,B,C) first compute the fare for Trip(A) [$20], then for Trip(A,B) -Trip(A) [$20+$15-$20 = $15], then for Trip(A,B,C) [$20+$15+$75-$15-$20 = $75]
- Order(C,A,B), we compute fares for Trip(C) [$100], then for Trip(C,A) — Trip(C) [$20+$85-$100 = $5], and Trip(C,A,B) [$20+$15+$75-$5-$100 = $5]
Note: Trip(X,Y) denotes the lowest fare to get to both destination X and Y (ie: min_fare( X=>Y, Y=>X)). For example, Trip(C,A) is the fare for dropping off at A first and then C, instead of the other way around, which is more expensive.
We will repeat the procedure for the other four permutations.
At last, we come to the solution of $10 for A, $15 for B, and $85 for C. GAME THEORY OPTIMAL. You will find that the result does indeed satisfy both fairness clauses.
Wrapping up
I always envy people who can utilize their professional skillset on their personal life. For example, professional chefs can make great meals at home, and software engineers can build smart homes using raspberry pi.
Well — I can split an Uber bill fair and square.
Kidding aside, I think it would be nice if Uber could implement a split fare feature based on Shapley value, but I imagine this will introduce more confusion than convenience.
Now, if you made it this far into the article, you may as well try this approach next time when you split an Uber with someone. I highly encourage it.
If you liked this article, feel free to connect with me on LinkedIn or Twitter.
Bonus: Is proportional split fair?
For the uninitiated — an alternative solution to fairly splitting the Uber bill could be to split proportionally by computing the cost percentage if the three rides are taken separately. See the illustration below.
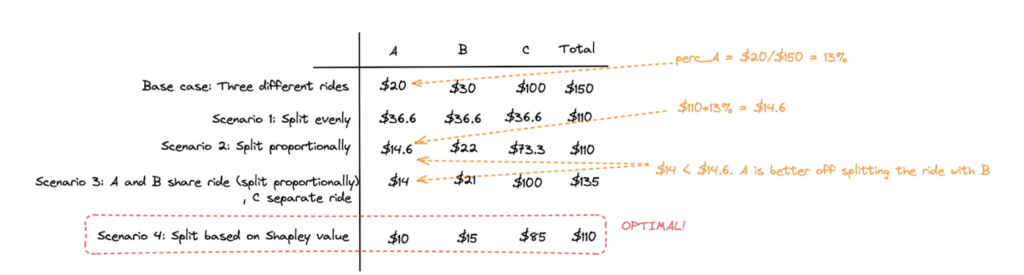
The problem with a proportional split is that it does not necessarily satisfy the pairwise rationality clause above. So in this example, A and B are better off taking a separate ride without C with a proportional split.
Reference
Game Theory Lecture II (5/6) Airport Problem: Application to Cost Allocation
